Até por volta do século XVI, os três graus do Oficio da Maçonaria, mais a continuação do terceiro grau conhecida como Real Arco, ainda continham resíduos de um desenvolvimento histórico das habilidades operativas dos antigos pedreiros livres e seus conhecimentos de geometria sagrada aprendida milênios antes.
Quase em todas as épocas evolutivas da sociedade humana os Mestres Maçons eram os desenhistas de quase todos os prédios importantes com os conhecimentos da geometria e a interpretação da astrologia seguindo padrões ancestrais milenares.
Desde o primeiro Templo de Jerusalém, denominado anos depois como o Templo de Salomão, períodos de construção Greco-Romanas e até a era Medieval com as grandes Catedrais, os maçons eram os únicos com o conhecimento SECRETO ou “Sabedoria Sagrada” capaz de construir estes magníficos, e até exuberantes, edifícios.
Estilo Românico:

É o estilo arquitetônico que surgiu na Europa no século X e evoluiu para o estilo gótico no fim do século XII. Caracteriza-se por construções austeras e robustas, com paredes grossas e minúsculas janelas, cuja principal função era resistir a ataques de exércitos inimigos.
O estilo é visto principalmente nas igrejas católicas construídas após a expansão do cristianismo pela Europa e foi o primeiro depois da queda do Império Romano a apresentar características comuns em várias regiões.
Estilo Gótico:
Arquitetura gótica é um estilo arquitetônico

que segundo pesquisas, é evolução da arquitetura românica. Com o gótico, a arquitetura ocidental atingiu um dos pontos culminantes da arquitetura pura. As abóbadas cada vez mais elevadas e maiores, não apoiavam-se em muros e paredes compactas e sim sobre pilastras ou feixes de colunas. Uma série de suportes que eram constituídos por arcobotantes e contrafortes possuíam a função de equilibrar de modo externo o peso excessivo das abóbadas. Desta forma, imensas paredes espessas foram excluídas dos edifícios de gênero gótico e foram substituídas por vitrais e rosáceas que iluminavam o ambiente interno.
O estilo gótico ficou marcado em muitas catedrais européias, entre elas a de Note-Drame, Chartres, Colônia, Amiens. Muitas catedrais góticas caracterizam-se pelo verticalismo e majestade, denominando-se durante a Idade Média, como supremacia e influência para a população.
Estilo Renascentista:

O Renascimento europeu, surgiu basicamente durante os séculos XIV, XV e XVI. Caracteriza-se por ser um momento de ruptura na História da Arquitetura em diversas esferas: nos meios de produção da arquitetura; na
linguagem arquitetônica adotada e na sua teorização. Caracteriza-se, também, por uma nova atitude dos arquitetos em relação à sua arte, passando a assumirem-se cada vez mais como profissionais independentes, portadores de um estilo pessoal. Saem as grandes paredes estruturais deixando edifícios mais leves e resistentes o que permite a entrada de grandes vãos para a construção de vitrais (armação de vidro e chumbo).
Desde o ponto de vista Arquitetônico cronológico poder-se-ia disser que os Maçons passarem de ser apenas pedreiros incultos, unidos por uma irmandade, ou fraternidade (sindicato), a clube de Cavalheiros e Arquitetos na era Renascentista deixando o caminho preparado para o grande evento de regularização da GLUI (Grande Loja Unida) de Inglaterra, em 1717.
Mas por trás de toda esta história devemos entender que sempre existiu um grupo de pessoas que possuía estes conhecimentos e ferramentas com as quais adquiriram liberdade, fama e fortuna.
O foco deste artigo é justamente o conhecimento inicial da geometria sagrada que levou ao inicio de nossa irmandade e que transformou a sociedade e sua arquitetura tal como a conhecemos hoje.
Antes do desenvolvimento de compilações aritméticas sofisticadas, a Geometria era uma importante ferramenta de resolução de problemas do tipo que hoje resolvemos facilmente como conseqüência de nosso entendimento matemático. Nossos ancestrais perceberam que três figuras geométrica – o quadrado, o círculo e o triângulo – formavam a base de quase todas as soluções de seus problemas particulares. O círculo era o mais respeitado de todos os símbolos geométricos, já que era uma linha que, sem começo definível, por tanto, sem fim, representava o infinito. O centro do círculo era o ponto mais respeitado, já que de cada parte da circunferência era eqüidistante, sendo o centro da criação , portanto, infinito em poder.
Um pino podia ser cravado no chão com uma corda ou um pano amarrado á ponta de uma estaca e á pessoa podia traçar um círculo no chão ao caminhar em volta da estaca. A partir de onde originasse , a circunferência do círculo podia então ser usada para estabelecer as quatro faces de um quadrado.
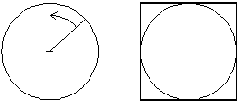 |
Os princípios da Geometria foram registrados em uma série de teoremas expostos pelo matemático grego Euclides por volta de 300 AEC. Um dos primeiros princípios a que ele faz alusão é o processo de dividir uma linha reta em duas partes iguais. Isso é feito pegando a linha AB e desenhando dois círculos de igual diâmetro, um circulo em cada ponta da linha, de modo que eles se sobreponham.
 |
O desenho de uma linha vertical entre os pontos C e D vai dividir em duas partes a linha AB, com dois comprimentos iguais.
Esse conceito pode ser obtido em um estágio suplementar, quando os círculos, ambos de igual diâmetro, são desenhados de tal modo que a circunferência de um toque o centro do outro círculo. Esse modelo geométrico era bem conhecido dos antigos e foi passado adiante, até nós, com o título de Vesica Piscis. A área resultante, onde os dois círculos se sobrepõem, é conhecida como a Vesica. Ela produz algumas características interessantes. Por exemplo: é possível a partir do uso desses dois círculos determinar um ângulo de 30 graus e de 60 graus.
Isso é mostrado no diagrama abaixo por meio de dois pontos, onde 60 graus é definido pelos pontos ABC. A linha em negrito, em ângulo, representa a hipotenusa de um triângulo reto CBA. Então, o ângulo oposto, BAC, é 30 graus. Ao transformar essa relação simples em um retângulo (como mostram as linhas pontilhadas) e ao dividir em dois os ângulos com um par de círculos, é possível criar os ângulos de 15; 30; 45; 60; 75 e 90 graus. Assim com um simples par de círculos e uma ponta reta, por exemplo um padrão ou régua de 24 polegadas, nossos ancestrais eram capazes de determinar os ângulos geométricos primários normalmente usados.
Essa estrutura geométrica simples imediatamente leva à construção de outra figura importante: o triângulo eqüilátero.
Assim, nossos ancestrais, por seus conhecimentos de geometria, eram capazes de produzir, com considerável exatidão, as três formas geométricas mais comuns em seu arsenal de construção: o círculo, o quadrado e o triângulo eqüilátero, os últimos dois sendo derivados da forma básica, o círculo. Então o circulo e a Vesica Piscis tornou-se um dispositivo geométrico altamente considerado. Esta geometria simples serviu de base para a construção de muitos templos, palácios,e prédios importantes de tempos antigos.
O conhecimento do potencial prático da Vesica Piscis seria de considerável utilidade para os construtores dos tempos antigos, pois permitia que dispositivos para a medição de ângulos de 30, 60 e 90 graus fossem desenvolvidos no local, bem melhor que carregar dispositivos incômodos de um lugar par outro. Muitas das plantas baixas para a construção de igrejas e monumentos importantes originaram-se dos princípios da Vesica Piscis.
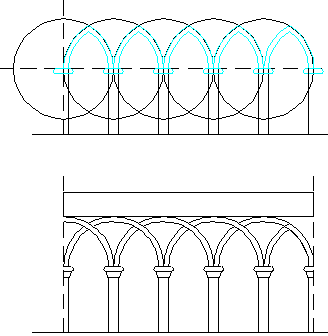
Outra das ferramentas decisivas na construção a partir da geometria foi a chegada do Arco ou arco gótico, característico das grandes catedrais da Europa que foram construídas entre os séculos XII e XIII. Os melhores exemplos podem ser encontrados nas catedrais de Canterbury e Cartres. Essa concepção foi usada pela primeira vez na Inglaterra na reconstrução da catedral de Canterbury depois que o prédio original foi destruído por um incêndio.
Todas as figuras que faziam parte da construção nessas épocas faziam referência ao Vesica. Portas e janelas, até os novos VITRO (armação de chumbo e vidro) deixarem a marca da Vesica.
 |

Outros símbolos geométricos também podem ser desenvolvidos a partir de círculos interligados. Entre estes havia um claramente associado ao rei Salmão, a Estela de Davi de seis pontas. O pentagrama ás vezes também é citado como o Selo de Salomão.
Embora seja um processo geométrico raramente falado no século XXI, a Vesica Piscis continua sendo usada ainda hoje. Ela pode freqüentemente ser exibida como um símbolo cristão.
Os antigos perceberam que deveria existir um relacionamento entre a circunferência e o diâmetro de um círculo, a razão que atualmente conhecemos como o número PI. Os egípcios ficaram conhecidos por ter definido a razão de 3:1, a razão que é encontrada em relação às colunas do Tempo de Salomão:
Com base na relação 3:1, a medição de 12 para a circunferência daria o diâmetro de quatro. Os egípcios sabiam, porém, que a razão exata era um pouco maior que o número três exato. Em sua tentativa de descobrir a razão exata, os egípcios procuraram um quadrado cuja dimensão lateral tivesse uma área equivalente à de um circulo específico. Isso era conhecido como enquadrar o círculo. Descobriu-se que o círculo com diâmetro de nove unidades (nove côvados) produzia a mesma área equivalente a um quadrado cujos lados mediam oito unidades (oito côvados). O nove dividido por oito (9/8) é igual a 1,125. Acredita-se que isso tenha dado a eles a razão constante de 3,125. Isso é extraordinariamente próximo do valor normal usado hoje em dia de 3,142, uma variação de apenas 0,5%. A medição de 3 1/8 (três e um oitavo) não era fácil, mas a medição de 12 ½ (12,5) era.
E 12,5 é um valor equivalente muito próximo do 4x π (Pi).
Havia ainda outro relacionamento numérico que parecia ser de particular interesse para os nossos ancestrais.
Assim como os números três, cinco e sete eram vistos como os mais comuns na natureza, também eles perceberam que o valor de Fi também poderia ser interpretado geometricamente. Enquanto a maioria dos caracteres aritméticos ou geométricos tem um número simples definível, o Fi tem dois valores numéricos: 1,618 e 0,618, que, por conveniência, são escritos simplesmente como 1,6 ou 0,6. O Fi também se tornou conhecido como a Proporção Áurea ou a Proporção Divina. É uma daquelas fascinantes característica geométricas que , mais uma vez, dificilmente ainda é mencionada hoje em dia, embora nossos ancestrais tenham usado essa proporção na construção de muitas das maiores e remanescentes estruturas da Antiguidade, como o Parthenon em Atenas, que as gerações posteriores aprenderam a respeitar. Os relacionamentos proporcionais empregados criam um efeito que determina que a estrutura esteja visualmente em harmonia.
Para entendermos isso, precisamos examinar aquilo que veio a ser chamado de a seqüência de Fibonacci. Em termos simples, a mesma começa com os primeiros números de nosso sistema de contagem, zero, um e dois. Se somamos 0+1, então a reposta é 1. Se agora adicionarmos ao mesmo o total anterior de 1, então teremos 3. Se continuarmos com esse formato, teremos a seguinte série de totais:
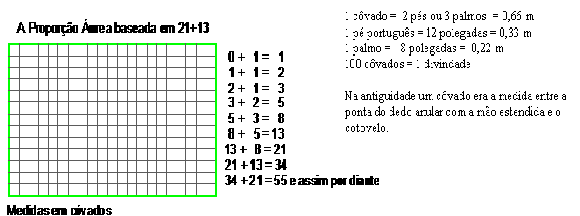 |
O Fi é uma característica encontrada extensivamente em proporções associadas á estrutura do corpo humano, como na relação entre o centro dos olhos e a largura da cabeça, a distância entre o cotovelo e o pulso, a proporção entre o comprimento do braço medido do ombro até o cotovelo, o resultado disso tudo é Fi, 1,618 (1,6).
Falando de um modo geral, uma estrutura construída com base no conceito de Fi tem proporções simétricas e agradáveis aos olhos da mesma maneira que muitos atributos da natureza são igualmente agradáveis. Estando relacionada com a natureza, essa estrutura, portanto, era vista como tendo a proporção preferida do Criador, e como tal érea uma criação divina, daí a expressão Proporção Divina.
|
Agora podemos criar dois círculos em Vesica Piscis, cada um representando 40 côvados de diâmetro ou 20 c de raio.
A linha regular (R) representa a hipotenusa
de um triângulo retângulo. A linha horizontal (A) é a base de um triângulo retângulo. Como a hipotenusa (R) é traçada a partir do centro para a circunferência do círculo, ela tem o comprimento igual ao raio 20.
A linha horizontal entre o círculos fica em um ponto que é a metade do raio. Assim, se o raio de um circulo completo for 20, então a metade do raio é 10.
Então, o lado vertical do triângulo é a metade do comprimento da linha vertical sólida (YZ).
Assim, aplicando o teorema de Pitágoras: a2 + b2 = c2 102 + b2 = 202 então, 202 – 102 = b2
então, 400 – 100 = 300 portanto, b=√300 = 17,32
A linha vertical (YZ) é o dobro do comprimento do lado vertical do triângulo
Assim: 17,32 x 2 = 34,64
Porém, deveria ser para uma razão de 1. Temos uma razão de 20.
34,64/20=1,732 = √3
As colunas possuem muitos secretos incorporados, mas um dos mais importantes é a sua medida em altura.
Na época antiga, e durante a construção do primeiro templo de Jerusalém, tinha-se muito em conta que Deus tinha criado o Universo em 7 dias e sendo cada dia muito importante. Por tanto a suma de todos estes dias produzia um número considerado Divino: 1+2+3+4+5+6+7= 28
 |
Daí passou-se a considerar como unidade de medida este número para determinar a altura dos ponteiros ou marcadores de sombra utilizados para todo tipo de cálculos. Por exemplo a medida básica dos raios ou circunferências dos circulo da Vesica Piscis com os quais foram criadas as plantas do Templo do Rei Salomão. Estes medidas foram originadas pela avaliação das sombras projetadas entre o Equinócio (máxima altura) e Solstício (mínima altura).

Cria-se assim a medida de 20c de raio ou 40c de diâmetro para os círculos que produziriam a Vesica Piscis. O templo do Rei Salomão tem 3 Vesicas de comprimento, o Santo dos Santos, dentro do templo, tem 20 x 20 x 20c, as colunas Joaquim e Boaz encontram-se separadas 40c do portal do templo.
As colunas e as circunferências foram combinadas de tal forma que nas distintas posições do sol fossem projetados raios de luz e sombras em todo o interior do templo. Estes ponteiros indicavam as diferentes épocas para coletar ou semear diferentes espécies...ação denominada como Calendário Sazonal.
Conclusão:
* O diâmetro do círculo da Vesica Piscis utilizado nos templos esta originada pela sombra projetada das colunas determinadas pelo Rei Salomão e combinadas com os solstícios e Equinócios.
* Existem constantes matemáticas nos desenhos da Vesica, tais como: √2; √3; √5
* A capacidade de exibir o valor de Fi= 1,618 e 0,618 como resultados finais nos retângulos obtidos.
E muitos outros itens não imediatamente óbvios, mas o que aconteceu com a sabedoria antiga? Ela precisa ser preservada. Ninguém sabe quando pode ser perdida pela sociedade em geral, e se vai precisar ser redescoberta.
* Textos e formulas obtidas do livro “Os segredos do Templo de Salomão” do escritor e irmão “Kevin L. Gest”
* Figuras redesenhadas por mim com o programa Auto Cad.
* Alguns conceitos obtidos da web e do Wikipédia
* Considerações pessoais e modificação de textos a terceira pessoa.
* Compilação do documento de minha autoria sem fins lucrativos





muito bom seu texto e bem ilustrado.
ResponderExcluir